El campo eléctrico producido por objetos cargados estáticos puede obtenerse por dos procedimientos equivalentes: mediante la ley de Coulomb o mediante la ley de Gauss, ley debida a Karl Friedrich Gauss (1777-1855) físico y matemático alemán que hizo muchas aportaciones a la física tanto teórica como experimental. En los dos capítulos anteriores se describió la ley de Coulomb y el potencial eléctrico, en este se presenta la ley de Gauss. La ley de Coulomb es una forma simple y directa de expresar la fuerza eléctrica. Por otro lado, la ley de Gauss es más sutil, más elegante y, a veces, más útil. La ley de Gauss requiere una sofisticación matemática mayor que la ley de Coulomb; pero, como recompensa, usándola se adquiere un conocimiento más profundo de la interacción eléctrica.
La ley de Gauss se puede aplicar para evaluar el campo eléctrico si la distribución de carga es suficientemente simétrica. Como se verá más adelante, si el campo eléctrico se conoce, la ley de Gauss se puede utilizar para calcular la carga que lo produce.
EL FLUJO.
La palabra flujo se deriva del latín fluxus, y éste de fluye, que significa fluir. Este concepto proviene de la teoría de fluidos, donde el flujo significa la rapidez con que un fluido pasa a través de una superficie imaginaria. Imaginémonos un tubo que conduce agua a velocidad constante. El volumen de agua que pasa por cualquier sección transversal A0 del tubo, por unidad de tiempo es:
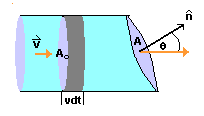
El mismo volumen sale de la superficie diagonal en el extremo del tubo. El flujo de salida se debe a la componente de velocidad .
Esta última ecuación se define como el flujo del campo de velocidades, denotado como:
El flujo de un campo vectorial involucra: (i) al campo; y (ii) a una superficie para la cual el flujo es evaluado. La superficie se representa mediante un vector superficie dado como
. Para una superficie plana el vector superficie tendrá un modulo A igual al área de la superficie, y como dirección un vector normal a la superficie.
El vector superficie presenta una ambigüedad en su definición, ya que existen dos direcciones perpendiculares, una opuesta a la otra. Esto se puede resolver fácilmente cuando la superficie es cerrada. Por superficie cerrada se entiende como aquella superficie que encierra un volumen, como en la misma figura 5.1. Siguiendo la costumbre, se escoge la dirección de siempre saliendo hacia afuera del volumen encerrado. Esto significa que la dirección en la cara de la derecha apunta como en ella se muestra, para la superficie de la izquierda apunta en la dirección contraria al campo de velocidades y para la otra superficie (cilíndrica) apunta saliendo en la dirección radial.